什么是“等式理论计划”
还是先来扒一扒陶哲轩这回究竟是整了个什么样的活儿。
简单说,“等式理论计划”是指:
采用”数学家+AI(包括自动定理证明系统和大模型)+证明辅助语言Lean”这样的协作方式,构建一个展示4694个magma等式(最多四次使用magma操作)之间所有蕴含关系的 “蕴含图”。
首先,这个计划的最初灵感源于陶哲轩本人对“去中心化”研究方式的畅想。
传统上,大部分数学研究项目都由少数专业数学家(通常1~5名)进行,每个人都对自己的部分更专业,且彼此可以相互验证。
不过也是因为存在验证环节,组织更大规模的数学项目(尤其是需要涉及公众贡献),一直具有挑战性。
而现在,通过AI工具以及Lean这样的证明辅助语言,数学项目的大规模协作变得可能。
打前阵的就有开源社区寻找梅森素数的成功尝试,在这个代号GIMPS的志愿项目中,任何拥有强大PC或GPU的人都可以加入寻找梅森素数。
虽然证明助手这样的AI工具在这个项目里用得还不多,但表达的精神是类似的。
因此,在开展等式理论计划之前,陶哲轩就打算搞一个实验:
在一个数学项目中,聚齐专业/业余数学家、AI工具、证明辅助语言Lean等,一同干大事!
受去年MathOverflow上一个等式问题的启发,这一次,陶哲轩将目光瞄准了代数领域中的magma。
当时的问题是酱婶儿的:
交换恒等式和常量恒等式之间是否存在等价关系?
抛开具体问题不谈,这里主要想说明magma涉及等式之间的关系。
简单来说,magma是一个代数结构,它由一个集合和一个在该集合上定义的二元运算组成,但不要求满足任何额外的代数性质,如结合律、交换律等。
我们常见的有关magma的等式包括:

而等式理论计划,就是要找出magma中不同等式之间的等价、推出和非推出关系。
就拿上面这11个等式来看,最终的关系图be like:
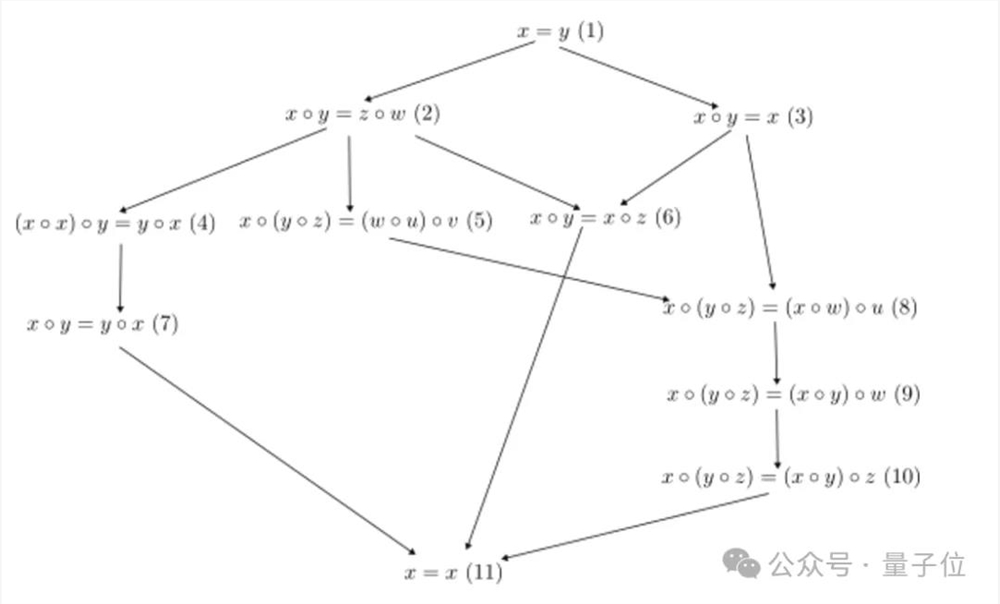
可以看出,常量公理等式(1)蕴含了其他所有等式,即如果1成立,那么其他等式也自动成立;而反身公理等式(11)由于最宽松(x=x),几乎所有的magma都满足这个公理。
回到计划本身,陶哲轩等人在初始阶段集中研究了那些只包含一个方程的magma定律,这些方程最多包含四个magma操作(即二元运算)。
举个例子,如果我们有一个magma(M,∗),其中M是元素的集合,∗是定义在M上的二元运算。
则一个“最多四次使用magma操作”的表达式如下:
a∗b(一次操作)
(
本文来自投稿,不代表金塔网立场,如若转载,请注明出处:https://www.jtagf.com/show_1813.html

 微信扫一扫
微信扫一扫